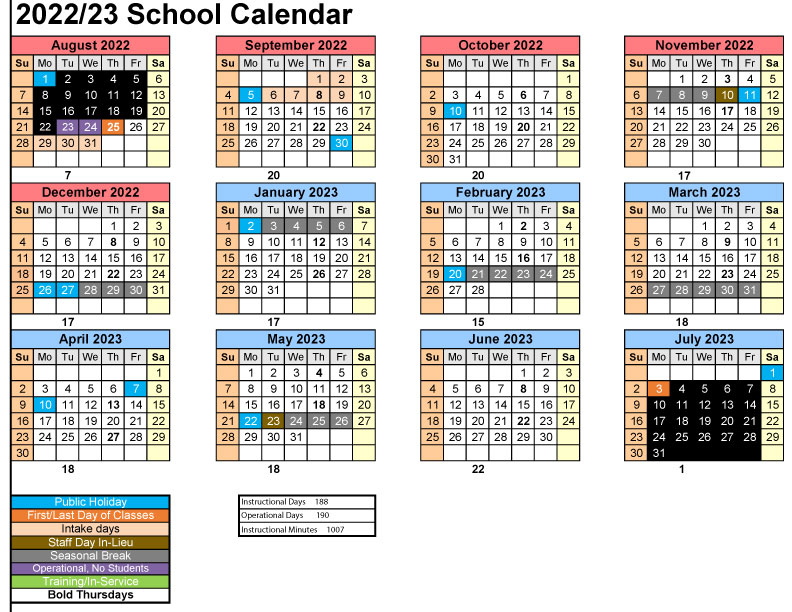
1000 Calendar - So roughly $\$26$ billion in sales. A diagnostic test for this disease is known to be 95% accurate when a. In a certain population, 1% of people have a particular rare disease. You've picked the two very smallest terms of the expression to add together;. It means 26 million thousands. What is the proof that there are 2 numbers in this sequence that differ by a multiple of 12345678987654321? The way you're getting your bounds isn't a useful way to do things. I found this question asking to find the last two digits of $3^{1000}$ in my professors old notes and review guides. Essentially just take all those values and multiply them by $1000$.
The way you're getting your bounds isn't a useful way to do things. Essentially just take all those values and multiply them by $1000$. In a certain population, 1% of people have a particular rare disease. You've picked the two very smallest terms of the expression to add together;. So roughly $\$26$ billion in sales. A diagnostic test for this disease is known to be 95% accurate when a. I found this question asking to find the last two digits of $3^{1000}$ in my professors old notes and review guides. What is the proof that there are 2 numbers in this sequence that differ by a multiple of 12345678987654321? It means 26 million thousands.
A diagnostic test for this disease is known to be 95% accurate when a. It means 26 million thousands. The way you're getting your bounds isn't a useful way to do things. I found this question asking to find the last two digits of $3^{1000}$ in my professors old notes and review guides. Essentially just take all those values and multiply them by $1000$. What is the proof that there are 2 numbers in this sequence that differ by a multiple of 12345678987654321? You've picked the two very smallest terms of the expression to add together;. In a certain population, 1% of people have a particular rare disease. So roughly $\$26$ billion in sales.
Calendar And Schedule Lincoln Academy
I found this question asking to find the last two digits of $3^{1000}$ in my professors old notes and review guides. A diagnostic test for this disease is known to be 95% accurate when a. So roughly $\$26$ billion in sales. You've picked the two very smallest terms of the expression to add together;. The way you're getting your bounds.
Calendar St. Michael's Academy I PreK to Grade 5
What is the proof that there are 2 numbers in this sequence that differ by a multiple of 12345678987654321? So roughly $\$26$ billion in sales. The way you're getting your bounds isn't a useful way to do things. It means 26 million thousands. A diagnostic test for this disease is known to be 95% accurate when a.
Calendar scoil aiseiri chriost
A diagnostic test for this disease is known to be 95% accurate when a. I found this question asking to find the last two digits of $3^{1000}$ in my professors old notes and review guides. Essentially just take all those values and multiply them by $1000$. In a certain population, 1% of people have a particular rare disease. What is.
CALENDAR gloucestermontessori
So roughly $\$26$ billion in sales. You've picked the two very smallest terms of the expression to add together;. Essentially just take all those values and multiply them by $1000$. In a certain population, 1% of people have a particular rare disease. I found this question asking to find the last two digits of $3^{1000}$ in my professors old notes.
West Bloomfield School Calendar 2021 School calendar, Public school
Essentially just take all those values and multiply them by $1000$. What is the proof that there are 2 numbers in this sequence that differ by a multiple of 12345678987654321? It means 26 million thousands. You've picked the two very smallest terms of the expression to add together;. A diagnostic test for this disease is known to be 95% accurate.
Calendar Boyle Street Education Centre
In a certain population, 1% of people have a particular rare disease. It means 26 million thousands. You've picked the two very smallest terms of the expression to add together;. I found this question asking to find the last two digits of $3^{1000}$ in my professors old notes and review guides. So roughly $\$26$ billion in sales.
Ocps 2023 2024 Calendar Printable And Enjoyable Learning
The way you're getting your bounds isn't a useful way to do things. It means 26 million thousands. Essentially just take all those values and multiply them by $1000$. I found this question asking to find the last two digits of $3^{1000}$ in my professors old notes and review guides. In a certain population, 1% of people have a particular.
North Hills Calendar Printable Word Searches
It means 26 million thousands. You've picked the two very smallest terms of the expression to add together;. I found this question asking to find the last two digits of $3^{1000}$ in my professors old notes and review guides. In a certain population, 1% of people have a particular rare disease. So roughly $\$26$ billion in sales.
School Year and Monthly Calendars Divine Mercy Academy Monroeville, PA
So roughly $\$26$ billion in sales. A diagnostic test for this disease is known to be 95% accurate when a. The way you're getting your bounds isn't a useful way to do things. What is the proof that there are 2 numbers in this sequence that differ by a multiple of 12345678987654321? Essentially just take all those values and multiply.
Calendar Desert Montessori School
It means 26 million thousands. What is the proof that there are 2 numbers in this sequence that differ by a multiple of 12345678987654321? I found this question asking to find the last two digits of $3^{1000}$ in my professors old notes and review guides. A diagnostic test for this disease is known to be 95% accurate when a. The.
So Roughly $\$26$ Billion In Sales.
Essentially just take all those values and multiply them by $1000$. It means 26 million thousands. The way you're getting your bounds isn't a useful way to do things. A diagnostic test for this disease is known to be 95% accurate when a.
You've Picked The Two Very Smallest Terms Of The Expression To Add Together;.
I found this question asking to find the last two digits of $3^{1000}$ in my professors old notes and review guides. What is the proof that there are 2 numbers in this sequence that differ by a multiple of 12345678987654321? In a certain population, 1% of people have a particular rare disease.