Parabola Transformational Form - Its general equation is of the form. A fixed point (the focus), and a fixed straight line (the directrix) Definition a parabola is a curve where any point is at an equal distance from: Definition and key elements a parabola is a symmetrical curve that is defined as the set of all points that are equidistant from a fixed point. A parabola refers to an equation of a curve, such that a point on the curve is equidistant from a fixed point and a fixed line. The parabola is a member of the family of conic sections. The parabola is an open curve that is a conic section produced by the intersection of a right circular cone and a plane parallel to an.
The parabola is a member of the family of conic sections. Its general equation is of the form. The parabola is an open curve that is a conic section produced by the intersection of a right circular cone and a plane parallel to an. Definition a parabola is a curve where any point is at an equal distance from: A fixed point (the focus), and a fixed straight line (the directrix) Definition and key elements a parabola is a symmetrical curve that is defined as the set of all points that are equidistant from a fixed point. A parabola refers to an equation of a curve, such that a point on the curve is equidistant from a fixed point and a fixed line.
Definition and key elements a parabola is a symmetrical curve that is defined as the set of all points that are equidistant from a fixed point. A fixed point (the focus), and a fixed straight line (the directrix) The parabola is an open curve that is a conic section produced by the intersection of a right circular cone and a plane parallel to an. The parabola is a member of the family of conic sections. A parabola refers to an equation of a curve, such that a point on the curve is equidistant from a fixed point and a fixed line. Its general equation is of the form. Definition a parabola is a curve where any point is at an equal distance from:
PPT Graphing Quadratic Functions using Transformational Form
The parabola is an open curve that is a conic section produced by the intersection of a right circular cone and a plane parallel to an. Its general equation is of the form. The parabola is a member of the family of conic sections. A fixed point (the focus), and a fixed straight line (the directrix) Definition and key elements.
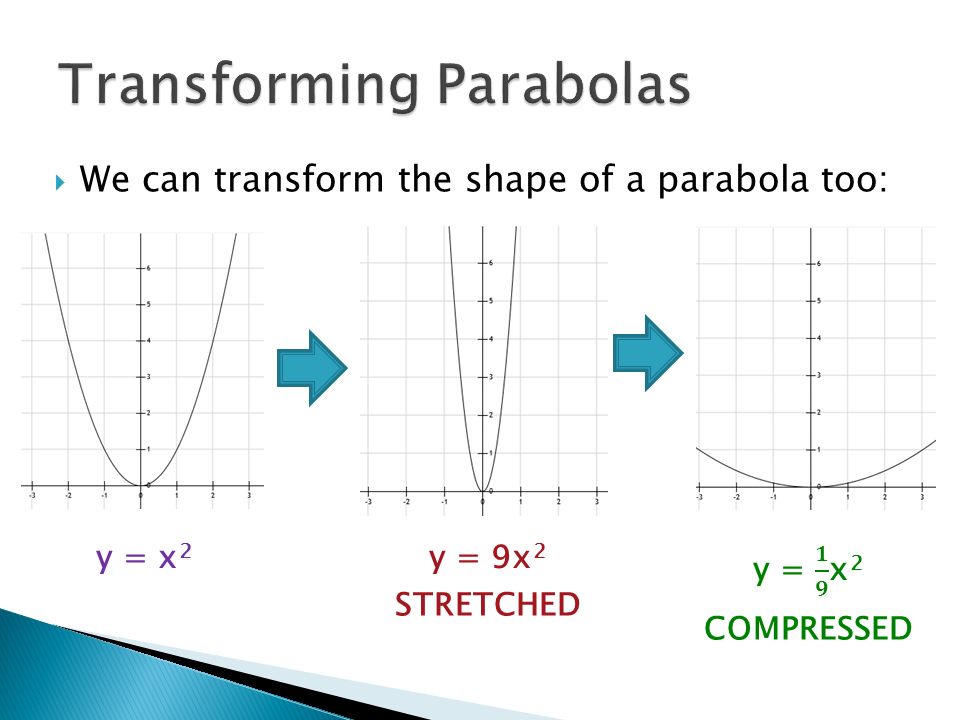
5.1 Stretching/Reflecting Quadratic Relations ppt download
The parabola is an open curve that is a conic section produced by the intersection of a right circular cone and a plane parallel to an. Definition a parabola is a curve where any point is at an equal distance from: A fixed point (the focus), and a fixed straight line (the directrix) The parabola is a member of the.
PPT Graphing Quadratic Functions Parabolas PowerPoint Presentation
The parabola is a member of the family of conic sections. A fixed point (the focus), and a fixed straight line (the directrix) A parabola refers to an equation of a curve, such that a point on the curve is equidistant from a fixed point and a fixed line. Definition and key elements a parabola is a symmetrical curve that.
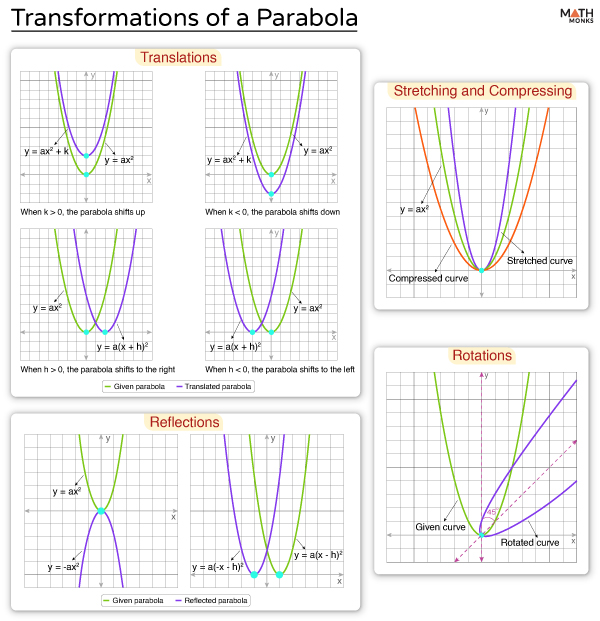
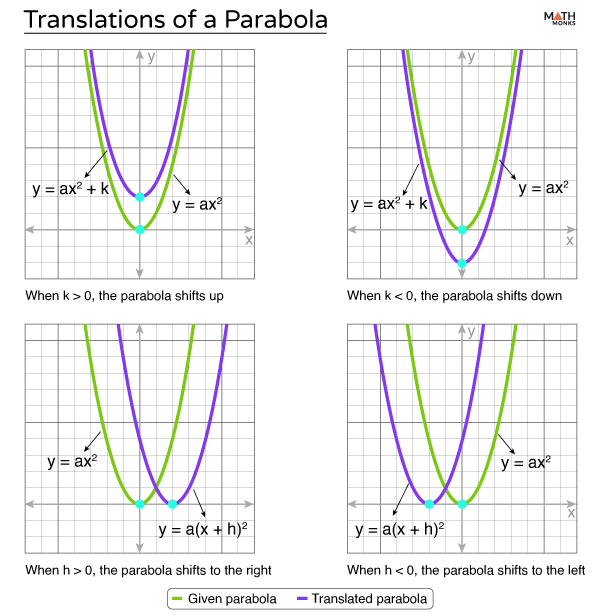
Transformations of a Parabola Examples & Diagrams
A fixed point (the focus), and a fixed straight line (the directrix) Definition and key elements a parabola is a symmetrical curve that is defined as the set of all points that are equidistant from a fixed point. Definition a parabola is a curve where any point is at an equal distance from: A parabola refers to an equation of.
Section 9.3 The Parabola. ppt download
A parabola refers to an equation of a curve, such that a point on the curve is equidistant from a fixed point and a fixed line. The parabola is a member of the family of conic sections. Its general equation is of the form. Definition and key elements a parabola is a symmetrical curve that is defined as the set.
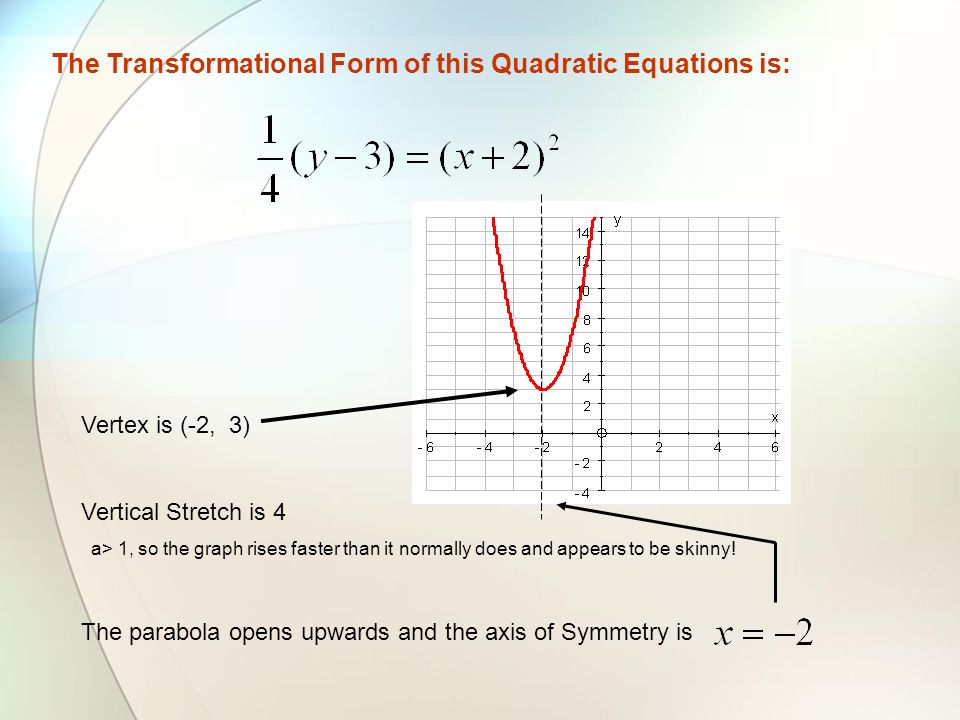
Quadratic Functions Transformational Form ppt download
The parabola is an open curve that is a conic section produced by the intersection of a right circular cone and a plane parallel to an. Its general equation is of the form. Definition and key elements a parabola is a symmetrical curve that is defined as the set of all points that are equidistant from a fixed point. Definition.
Solved Transformations Parabolas Revisited Vertex Form y=a(xh)^2+k
Definition a parabola is a curve where any point is at an equal distance from: A parabola refers to an equation of a curve, such that a point on the curve is equidistant from a fixed point and a fixed line. Its general equation is of the form. Definition and key elements a parabola is a symmetrical curve that is.
Transformations of a Parabola Examples & Diagrams
Definition a parabola is a curve where any point is at an equal distance from: A fixed point (the focus), and a fixed straight line (the directrix) Its general equation is of the form. A parabola refers to an equation of a curve, such that a point on the curve is equidistant from a fixed point and a fixed line..
[Solved] write the transformational form of the parabola with a focus
Definition a parabola is a curve where any point is at an equal distance from: Definition and key elements a parabola is a symmetrical curve that is defined as the set of all points that are equidistant from a fixed point. A fixed point (the focus), and a fixed straight line (the directrix) The parabola is an open curve that.
Graphing Quadratic Functions using Transformational Form The
The parabola is an open curve that is a conic section produced by the intersection of a right circular cone and a plane parallel to an. Its general equation is of the form. Definition a parabola is a curve where any point is at an equal distance from: A fixed point (the focus), and a fixed straight line (the directrix).
A Parabola Refers To An Equation Of A Curve, Such That A Point On The Curve Is Equidistant From A Fixed Point And A Fixed Line.
The parabola is a member of the family of conic sections. The parabola is an open curve that is a conic section produced by the intersection of a right circular cone and a plane parallel to an. Definition and key elements a parabola is a symmetrical curve that is defined as the set of all points that are equidistant from a fixed point. Definition a parabola is a curve where any point is at an equal distance from:
A Fixed Point (The Focus), And A Fixed Straight Line (The Directrix)
Its general equation is of the form.


.jpg)